Matemáticas. Unidad 4. Números primos y compuestos

 

 





   Un número primo es un número entero mayor que cero, que tiene exactamente dos divisores. También podemos definirlo como aquel número entero positivo que no puede expresarse como producto de dos números enteros positivos más pequeños que él, o bien, como producto de dos enteros positivos de más de una forma. Conviene observar que con cualquiera de las dos definiciones el 1 queda excluido del conjunto de los números primos.

    Ejemplos: a) El 7 es primo. Sus únicos divisores son 1 y 7. Sólo puede expresarse como producto de 7·1.
                    b) El 15 no es primo. Sus divisores son 1, 3, 5 y 15. Puede expresarse como 3·5. (y también como 15·1)

  

    Los 25 primeros números primos son 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97, que son todos los primos menores que 100.

    En la siguiente tabla tenemos todos los primos menores que 1000, que hacen un total de 168 (21×8)

2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71	73
79	83	89	97	101	103	107	109	113	127	131	137	139	149	151	157	163	167	173	179	181
191	193	197	199	211	223	227	229	233	239	241	251	257	263	269	271	277	281	283	293	307
311	313	317	331	337	347	349	353	359	367	373	379	383	389	397	401	409	419	421	431	433
439	443	449	457	461	463	467	479	487	491	499	503	509	521	523	541	547	557	563	569	571
577	587	593	599	601	607	613	617	619	631	641	643	647	653	659	661	673	677	683	691	701
709	719	727	733	739	743	751	757	761	769	773	787	797	809	811	821	823	827	829	839	853
857	859	863	877	881	883	887	907	911	919	929	937	941	947	953	967	971	977	983	991	997

Póster con los números primos hasta 1000 (pdf)     Listado con los primos menores que 1.000.000 (txt) 

Para ver los 10.000 primeros números primos pincha aquí

Primos en el anillo de los enteros de Gauss

Cómo averiguar si un número es primo.

    El algoritmo más sencillo que puede utilizarse para saber si un número n es primo es el de la división. Se trata de ir probando para ver si tiene algún divisor propio. Para ello vamos dividiendo el número n entre 2, 3, 4, 5, ... , n-1. Si alguna de las divisiones es exacta (da resto cero) podemos asegurar que el número n es compuesto. Si ninguna de estas divisiones es exacta, el número n es primo. 

                                                                             

NÚMEROS PRIMOS Y COMPUESTOS

NÚMEROS PRIMOS

 

MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR

PON A PRUEBA TUS CONOCIMIENTOS DE MCM Y MCD

Todo número compuesto se puede expresar de forma única como producto de distintos números primos elevados a potencias. Este procedimiento se llama factorización. Debemos dominarlo para poder hallar el mínimo común múltiplo y el máximo común divisor de números grandes.

 


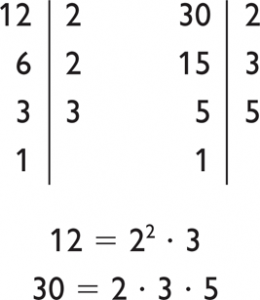
Ahora prueba tú...